Backpropagation DNN exercises

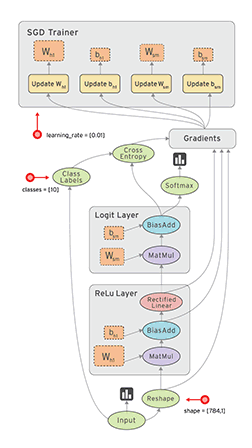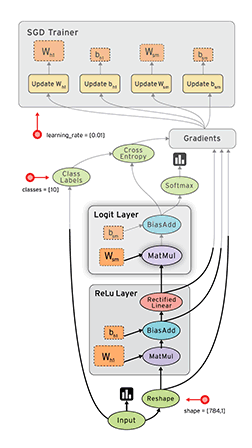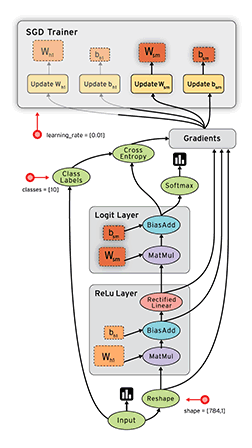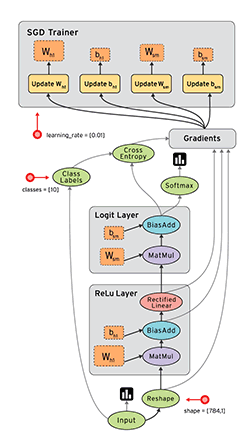
Computational graph in Tensorboard showing the components involved in a TF BP update

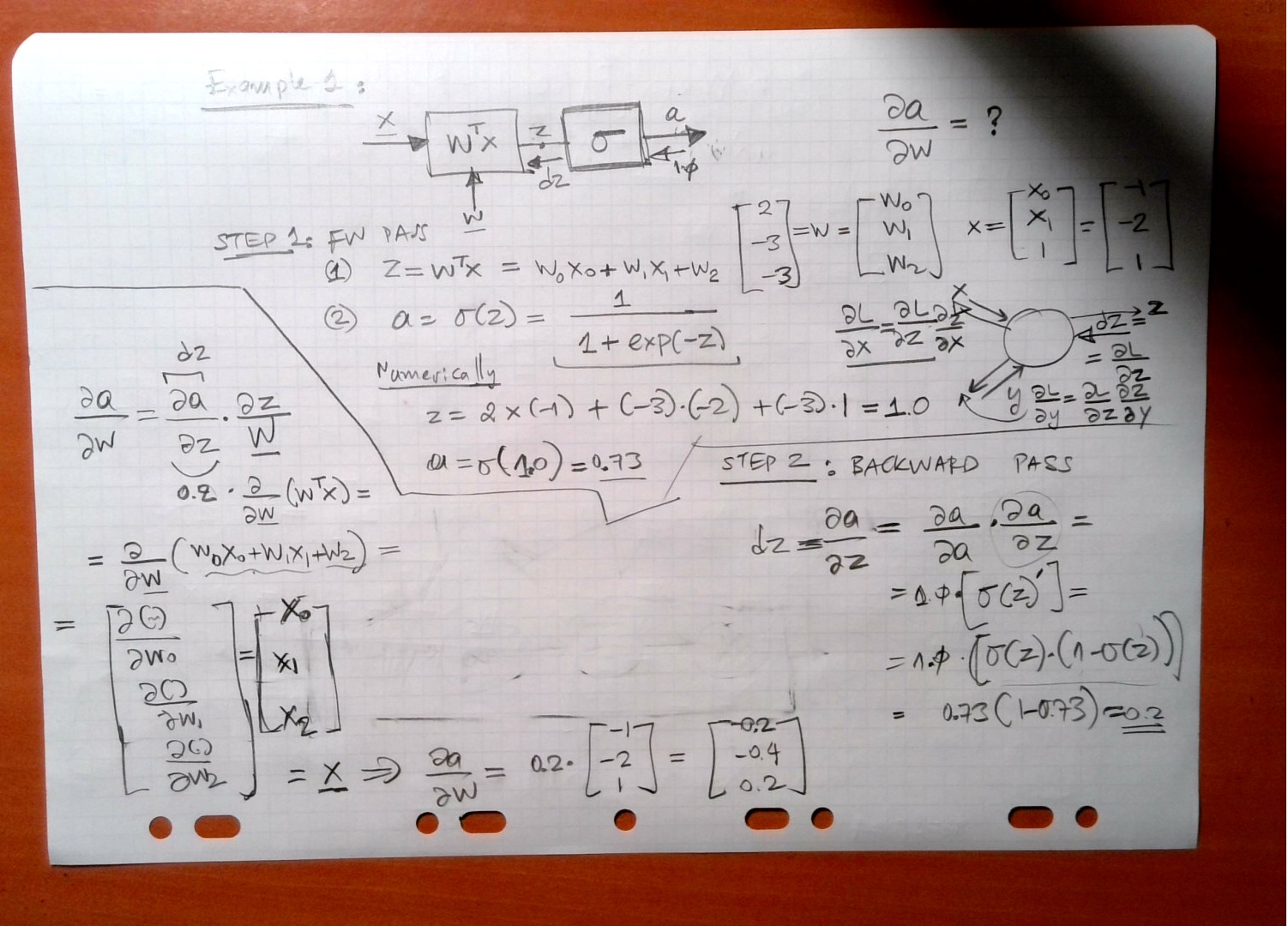
Neuron

backprop-neuron

Simple DNN 1

backprop-simple-dnn

Simple DNN 2

A network consist of a concatenation of the following layers

1. Fully Connected layer with input \(x^{(1)}\), \(W^{(1)}\) and output \(z^{(1)}\).
2. RELU producing \(a^{(1)}\)
3. Fully Connected layer with parameters \(W^{(2)}\) producing \(z^{(2)}\)
4. SOFTMAX producing \(\hat{y}\)
5. Cross-Entropy (CE) loss producing \(L\)

The task of backprop consists of the following steps:

1. Sketch the network and write down the equations for the forward path.
2. Propagate the backwards path i.e. make sure you write down the expressions of the gradient of the loss with respect to all the network parameters.

NOTE: Please note that we have omitted the bias terms for simplicity.

Forward Pass Step	Symbolic Equation
(1)	\(z^{(1)} = W^{(1)} x^{(1)}\)
(2)	\(a^{(1)} = \max(0, z^{(1)})\)
(3)	\(z^{(2)} = W^{(2)} a^{(1)}\)
(4)	\(\hat{y} = \mathtt{softmax}(z^{(2)})\)
(5)	\(L = CE(y, \hat{y})\)

Backward Pass Step	Symbolic Equation
(5)	\(\frac{\partial L}{\partial L} = 1.0\)
(4)	\(\frac{\partial L}{\partial z^{(2)}} = \hat y - y\)
(3a)	\(\frac{\partial L}{\partial W^{(2)}} = a^{(1)} (\hat y - y)\)
(3b)	\(\frac{\partial L}{\partial a^{(1)}} = W^{(2)} (\hat y - y)\)
(2)	\(\frac{\partial L}{\partial z^{(1)}} = \frac{\partial L}{\partial a^{(1)}}\) if \(a^{(1)} > 0\)
(1)	\(\frac{\partial L}{\partial W^{(1)}} = \frac{\partial L}{\partial z^{(1)}} \times x^{(1)}\)