Skip to main content
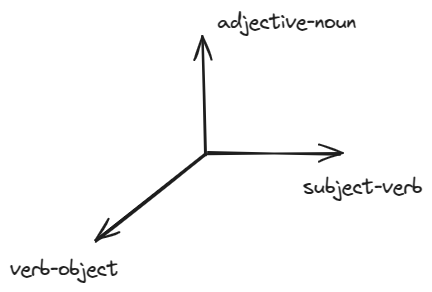
Earlier we have seen examples with the token bear being in multiple grammatical patterns that also influence its meaning. For example, we have seen the subject-verb-object pattern and the subject-verb-adjective-subject pattern. To capture such multiplicities we can use multiple attention heads where each attention head learns a different pattern such as the three shown in figure below. Axes of the attention heads in a multi-head attention mechanism. Each head learns a different pattern, such as subject-verb-object, subject-verb-adjective-subject, and subject-verb-adverb-object. This is just an analogy though and it could be valid in the first few blocks of the transformer. Think of the multiple heads in transformer architectures to be analogous to the multiple filters we use in CNNs. if HH is the number of heads, indexed by hh, then each head delivers Hh=Attention(Qh,Kh,Vh)H_h = \mathtt{Attention}(Q_h, K_h, Vh) where Qh,Kh,VhQ_h, K_h, V_h are the query, key and value matrices of the h−thh-th head. Qh=XWhqQ_h = X W_h^q Kh=XWhkK_h = X W_h^k Vh=XWhvV_h = X W_h^v where Whq,Whk,WhvW_h^q, W_h^k, W_h^v are the weight matrices of the h−thh-th head. The output of the multi-head attention is then given by X^=concat(H1,H2,...,HH)Wo\hat X = \mathtt{concat}(H_1, H_2, ..., H_H)W^o where WoW^o is the output weight matrix with dimensions Hdv×dH d_v \times d and typically dv=d/Hd_v = d/H. Multi-head attention mechanism. Each head learns a different pattern, and the output is a concatenation of the outputs of all heads, followed by a linear transformation with the weight matrix WoW^o that we call mixing matrix since it mixes / combines the outputs of the heads. The WoW^o matrix and the Whq,Whk,WhvW_h^q, W_h^k, W_h^v matrices are learned during training. The complexity of running multiple heads does not scale with the number of heads since as you can also see in the code below we divide the head-size by the number of heads, avoiding a corresponding increase in the number of parameters. 
class MultiHeadAttention(nn.Module):
    def __init__(self, config):
        super().__init__()
        embed_dim = config.hidden_size
        num_heads = config.num_attention_heads
        head_dim = embed_dim // num_heads
        self.heads = nn.ModuleList(
            [AttentionHead(embed_dim, head_dim) for _ in range(num_heads)]
        )
        self.output_linear = nn.Linear(embed_dim, embed_dim)

    def forward(self, hidden_state):
        x = torch.cat([h(hidden_state) for h in self.heads], dim=-1)
        x = self.output_linear(x)
        return x

​
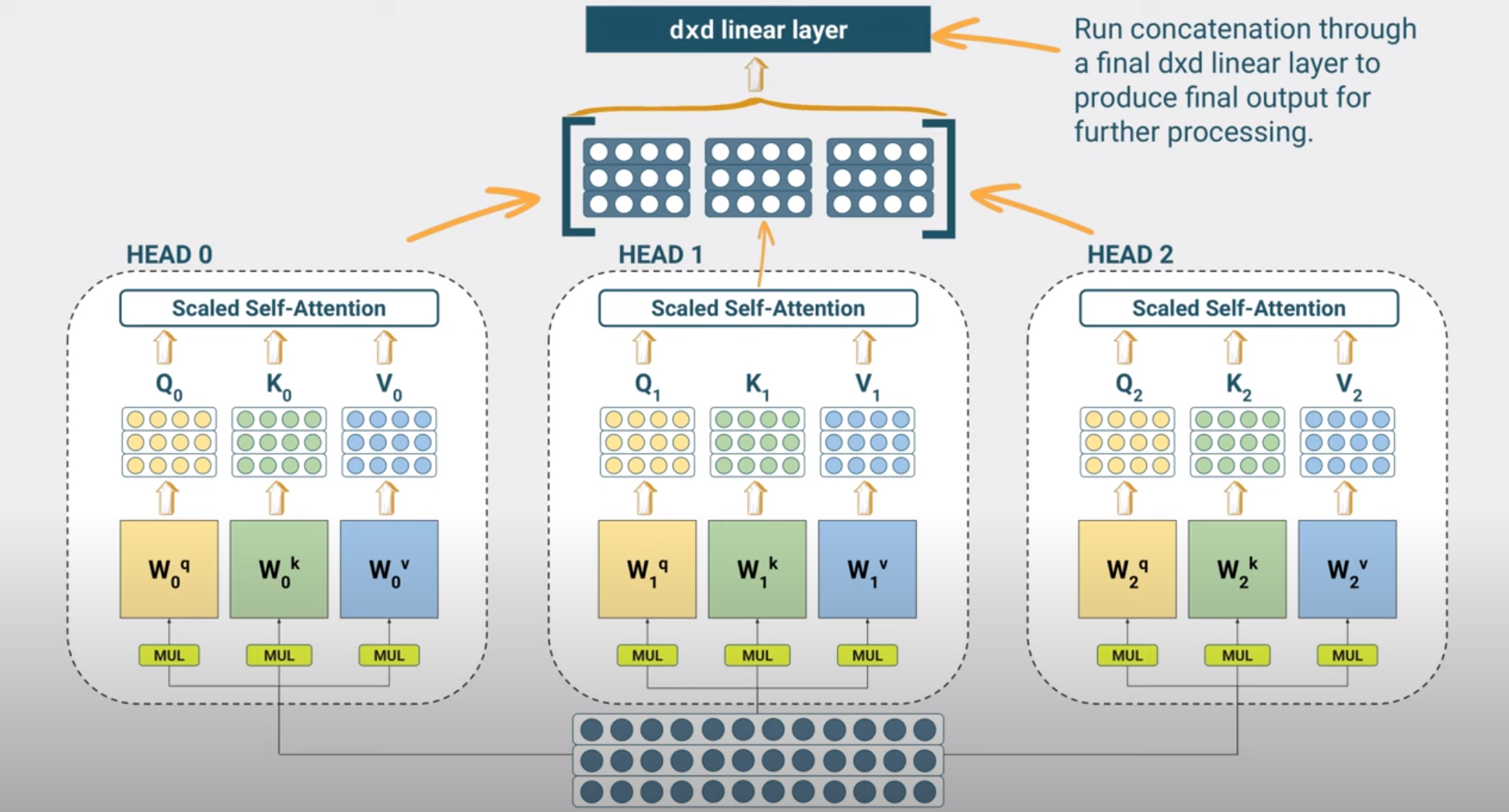
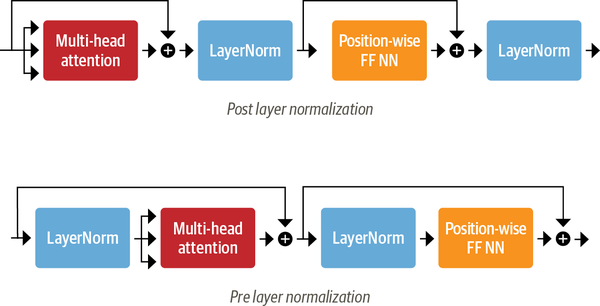
Attention Blocks with Skip Connections

Layer Normalization is a technique that normalizes the inputs across the features for each individual example, rather than across the batch. This helps stabilize the learning process and can lead to faster convergence. Layer Normalization has been shown to improve training efficiency and therefore we apply layer normalization to the input of the multihead self attention (MHSA). Z=LayerNorm(X^)Z = \mathtt{LayerNorm}(\hat X) In addition we borrow the same idea we have seen from ResNet, and add a skip connection from the input to the output of the MHSA. Z^=MHSA(Z)+X^\hat Z = \mathtt{MHSA}(Z) + \hat X We call the above block an attention block and since we know that depth helps in representations learning, we therefore want to stack multiple attention blocks, but before we do so we apply a feedforward layer to the output of each attention block for the reasons we describe below. Key references: (Lu et al., 2016; Wang et al., 2016; Andreas et al., 2015; Dauphin et al., 2016; Luong et al., 2015)

​
References

  • Andreas, J., Rohrbach, M., Darrell, T., Klein, D. (2015). Neural Module Networks.
  • Dauphin, Y., Fan, A., Auli, M., Grangier, D. (2016). Language Modeling with Gated Convolutional Networks.
  • Lu, J., Xiong, C., Parikh, D., Socher, R. (2016). Knowing When to Look: Adaptive Attention via A Visual Sentinel for Image Captioning.
  • Luong, M., Pham, H., Manning, C. (2015). Effective Approaches to Attention-based Neural Machine Translation.
  • Wang, J., Yang, Y., Mao, J., Huang, Z., Huang, C., et al. (2016). CNN-RNN: A Unified Framework for Multi-label Image Classification.
Edit this page on GitHub or file an issue.