Skip to main content
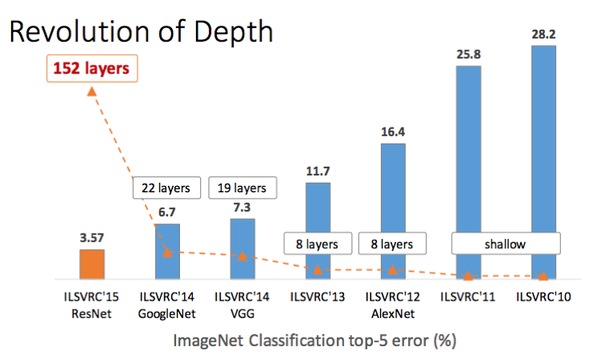
In the figure below we plot the top-5 classification error as a function of depth in CNN architectures. Notice the big jump due to the introduction of the ResNet architecture. Top-5 classification error as a function of CNN depth. Imagenet benchmarking The aim of this section is to provide an alternative view as to why ResNets seem to be able to accommodate much deeper architecture while performing even better that existing architectures for the same depth (e.g. ResNet-18).

​
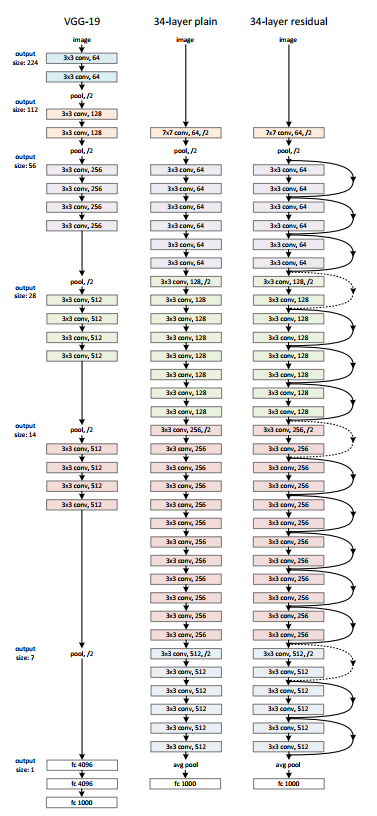
The ResNet Architecture

34 layers deep ResNet architecture vs. earlier architectures ResNets or residual networks, introduced the concept of the residual. This can be understood looking at a small residual network of three stages. The striking difference between ResNets and earlier architectures are the skip connections. Shortcut connections are those skipping one or more layers. The shortcut connections simply perform identity mapping, and their outputs are added to the outputs of the stacked layers. Identity shortcut connections add neither extra parameter nor computational complexity. The entire network can still be trained end-to-end by SGD with backpropagation, and can be easily implemented using common libraries without modifying the solvers. Unrolling the residual architecture.

​
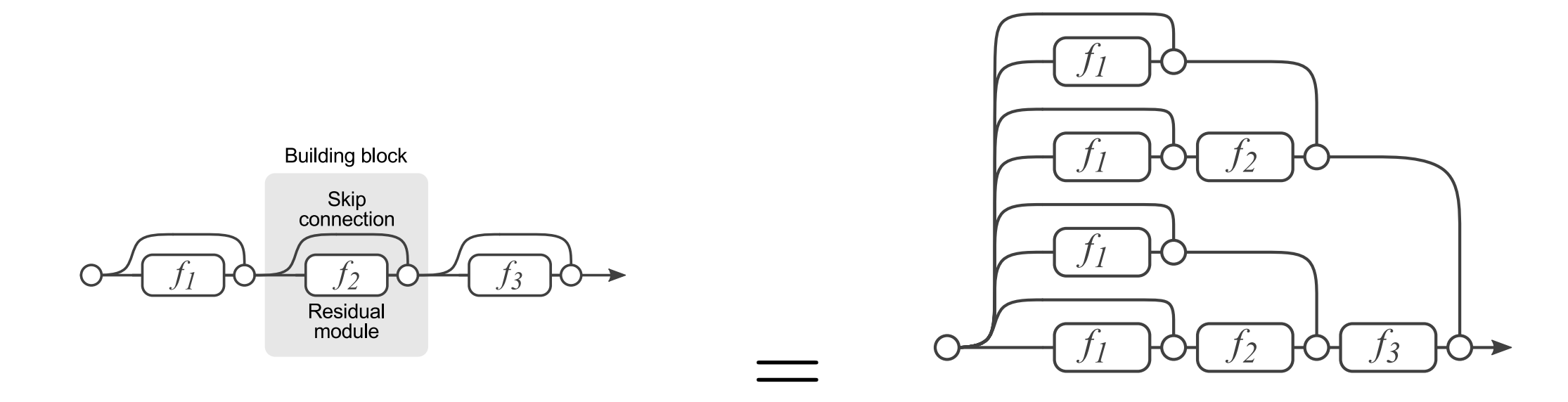
Performance advantages of ResNets

Hinton showed that using dropout, dropping out individual neurons during training, leads to a network that is equivalent to averaging over an ensemble of exponentially many networks.We now show that similar ensemble learning performance advantages are present in residual networks. To do so, we use a simple 3-block network where each layer consists of a residual module fif_i and a skip connection bypassing fif_i. Since layers in residual networks can comprise multiple convolutional layers, we refer to them as residual blocks. With yi−1y_{i-1} as is input, the output of the i-th block is recursively defined as yi=fi(yi−1)+yi−1y_i = f_i(y_{i−1}) + y_{i−1} where fi(x)f_i(x) is some sequence of convolutions, batch normalization, and Rectified Linear Units (ReLU) as nonlinearities. In the figure above we have three blocks. Each fi(x)f_i(x) is defined by fi(x)=Wi(1)∗ReLU(B(Wi(2)∗RELU(B(x))))f_i(x) = W_i^{(1)} * ReLU(B (W_i^{(2)} * RELU(B(x)))) where Wi(1)W_i^{(1)} and Wi(2)W_i^{(2)} are weight matrices, · denotes convolution, B(x)B(x) is batch normalization and RELU(x)≡max⁡(x,0)RELU(x) ≡ \max(x, 0). Other formulations are typically composed of the same operations, but may differ in their order. This paper analyses the unrolled network and from that analysis we conclude on mainly three advantages of the architecture:
  1. We see many diverse paths to the gradient as it flows from the y^\hat y to the trainable parameter tensors of each layer.
  2. We see elements of ensemble learning in the formation of the hypothesis y^\hat y.
  3. We can eliminate layers from the architecture (blocks) without having to redimension the network, allowing us to trade performance for latancy during inference.
ResNets are commonly used as feature extractors for object detection as in this tutorial. These networks are a defacto choice today as featurization / backbone networks and they are also extensively used in real time applications.

​
ResNets and Batch Normalization

This notebook is very instructive of what now is considered a canonical new ResNet block that includes batch normalization.
Edit this page on GitHub or file an issue.
Connect these docs to Claude, VSCode, and more via MCP for real-time answers.