Skip to main content

​
Input Normalization and its Limitations

We have traditionally normalized input data to have a mean of 0 and standard deviation of 1. This ensures the input data is centered and has similar scale, making optimization stable and faster.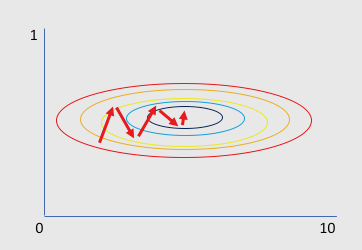
SGD convergence
In this contour plot, the SGD trajectory is not smooth, meaning the algorithm converges slowly. The gradient with respect to one parameter dominates the direction, creating a zig-zag pattern. Normalizing the input is effective but not enough. The distribution of activations also changes as data propagates through the network, affected by parameter values.

​
Parameter Initialization

Various techniques address this issue, such as careful weight initialization or activation functions less sensitive to weight scale. Common initializers include:
  • Random Normal: Standard normal distribution
  • Glorot/Xavier: Scaled for sigmoid/tanh activations
  • He: Scaled for ReLU activations

​
Batch Normalization

Batch Normalization (Bjorck et al., 2018) alleviates headaches with weight initialization by explicitly forcing activations to have a specific distribution during training.

​
Normalization Step

Normalizes the input to each layer so activations have zero mean and unit variance: x^=x−μbatchσbatch2+ϵ\hat{x} = \frac{x - \mu_{\text{batch}}}{\sqrt{\sigma_{\text{batch}}^2 + \epsilon}} Where:
  • μbatch\mu_{\text{batch}} is the mean of the mini-batch
  • σbatch2\sigma_{\text{batch}}^2 is the variance of the mini-batch
  • ϵ\epsilon is a small value to prevent division by zero

​
Scaling and Shifting

After normalization, activations are scaled and shifted using learnable parameters γ\gamma and β\beta: y=γx^+βy = \gamma \hat{x} + \beta This allows the network to recover any input distribution while keeping it stable.

​
Intuition of Batch Normalization

During backpropagation, the gradient of a neuron’s output with respect to its parameters is proportional to the input. Controlling the statistics of what the previous layer produces (input to current layer) ensures gradients are appropriate. The learnable parameters γ\gamma and β\beta let the network determine what’s optimal.

​
Effects of Batch Normalization

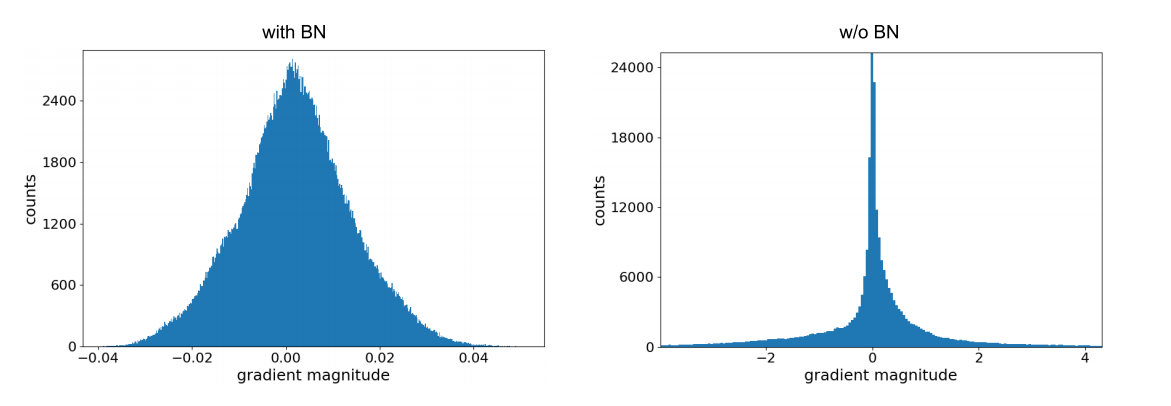
Histograms with and without BN
Benefits:
  • Faster convergence
  • Allows higher learning rates
  • Reduces sensitivity to parameter initialization
  • More robust training

​
Implementation Notes

  • During training: compute mean and variance from mini-batch
  • During inference: use running mean and variance (accumulated during training)
  • Typically applied after convolutional/fully connected layers, before or after activations
Networks with Batch Normalization are significantly more robust to parameter initialization. BN can be interpreted as doing preprocessing at every layer, integrated into the network in a differentiable manner.

​
References

Edit this page on GitHub or file an issue.
Connect these docs to Claude, VSCode, and more via MCP for real-time answers.