Skip to main content
Layer Normalization vs Batch Normalization

​
Limitations of Batch Normalization

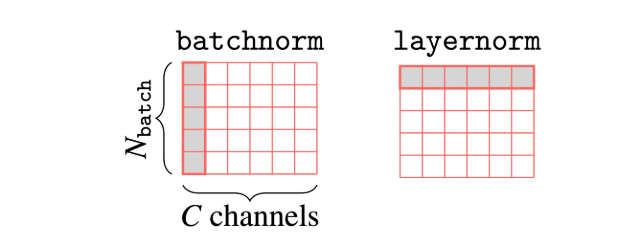
Batch Normalization (BN) helps training efficiency by positioning activations in a trainable way. However, it has limitations with small batch sizes since it operates across the batch dimension and normalizes activations for each feature/channel across the batch. Smaller batch sizes result in inaccurate statistics. This is particularly problematic in LLMs that require small mini-batches due to memory constraints.

​
Layer Normalization

For architectures such as recurrent networks and transformers, we apply Layer Normalization. The layer normalization of an input vector x∈Rdx \in \mathbb{R}^d is computed as: LayerNorm(x)=γ⊙x−μσ2+ϵ+β\text{LayerNorm}(x) = \gamma \odot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta where the mean μ\mu and variance σ2\sigma^2 are: μ=1d∑i=1dxi,σ2=1d∑i=1d(xi−μ)2\mu = \frac{1}{d} \sum_{i=1}^{d} x_i, \quad \sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2 Here:
  • γ\gamma and β\beta are learnable parameters (of shape dd)
  • ϵ\epsilon is a small constant for numerical stability
  • ⊙\odot denotes element-wise multiplication

​
Key Difference from Batch Normalization

Layer Normalization operates across the feature dimensions for each sample independently, normalizing the activations in a trainable way. This is effectively the transpose of Batch Normalization:
AspectBatch NormalizationLayer Normalization
Normalizes acrossBatch dimensionFeature dimension
Depends onBatch sizeIndependent of batch
Best forCNNs, large batchesRNNs, Transformers, small batches
Training vs InferenceDifferent behaviorSame behavior

​
When to Use Layer Normalization

  • Recurrent Neural Networks (RNNs): Variable sequence lengths make BN difficult
  • Transformers: Self-attention mechanisms benefit from LN
  • Small batch training: When memory constraints limit batch size
  • Online learning: Single-sample updates

​
References

Edit this page on GitHub or file an issue.
Connect these docs to Claude, VSCode, and more via MCP for real-time answers.