Covariance and Correlation Matrices

This notebook has been published on KDnuggets.

​

From covariance matrix to image whitening

The goal of this notebook is to go from the basics of data preprocessing to modern techniques used in machine learning. We can use code (Python/Numpy) to better understand abstract mathematical notions - thinking by coding! We will start with basic but very useful concepts in data science and machine learning like variance and covariance matrix and we will go further to some preprocessing techniques used to feed images into neural networks. We will try to get more concrete insights using code to actually see what each equation is doing. We call preprocessing all transformations on the raw data before it is fed to the machine learning algorithm. For instance, training a convolutional neural network on raw images will probably lead to bad classification performances (Pal & Sudeep, 2016). The preprocessing is also important to speed up training (see Lecun et al., 2012; section 4.3). Syllabus:

1. Background: Reminders about variance and covariance, generating and plotting fake data
2. Preprocessing: Mean normalization, standardisation and whitening
3. Whitening images: Zero Component Analysis (ZCA) for image preprocessing

​

1. Background

​

A. Variance and covariance

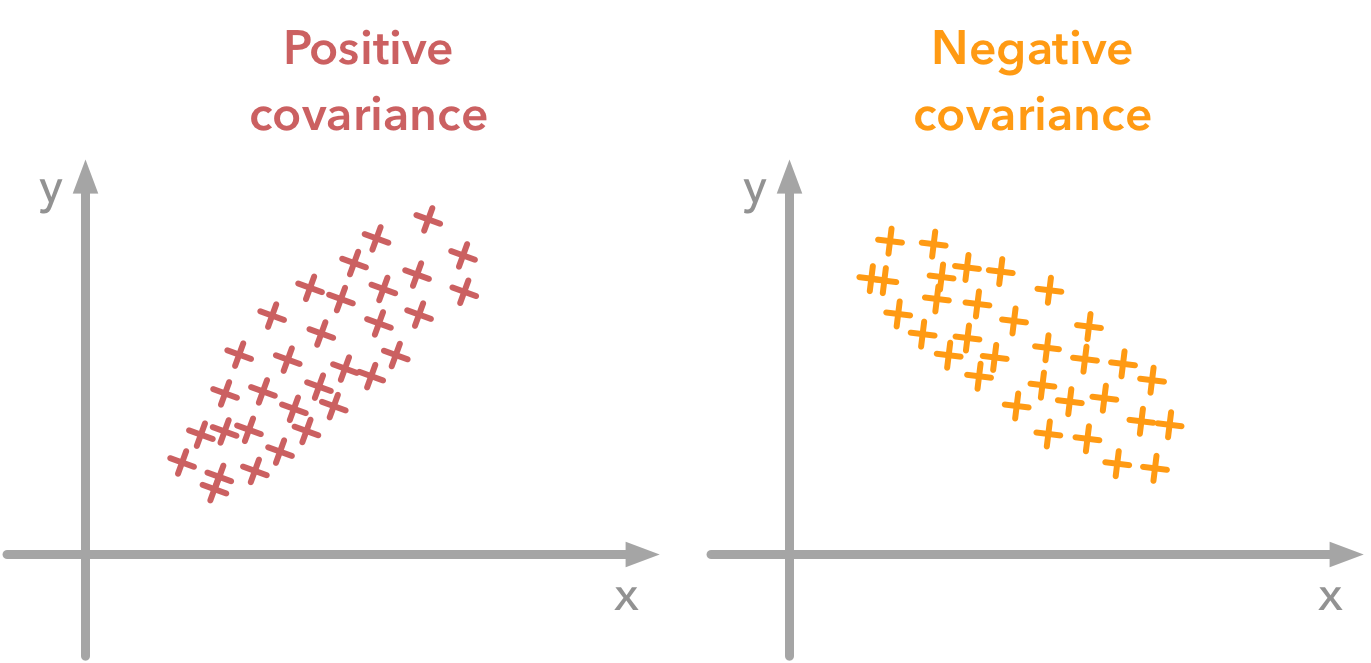
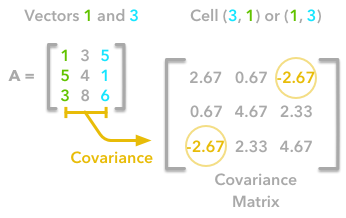
The variance of a variable describes how much the values are spread. The covariance is a measure that tells the amount of dependency between two variables. A positive covariance means that values of the first variable are large when values of the second variables are also large. A negative covariance means the opposite. The covariance matrix summarizes the variances and covariances of a set of vectors. The diagonal corresponds to the variance of each vector: The variance formula: $$V(\mathbf{X}) = \frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2$$ The covariance formula between two variables $\mathbf{X}$ and $\mathbf{Y}$: $$\text{cov}(\mathbf{X},\mathbf{Y}) = \frac{1}{n} \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})$$

​

Finding the covariance matrix with the dot product

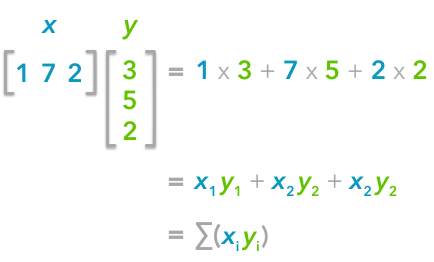
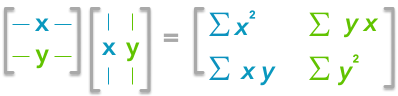
The dot product between two vectors: $$\mathbf{X}^\text{T}\mathbf{Y}= \sum_{i=1}^{n}(x_i)(y_i)$$ If we start with a zero-centered matrix, the dot product between this matrix and its transpose gives us the covariance matrix:

​

2. Preprocessing

​

A. Mean normalization

Mean normalization removes the mean from each observation, centering the data around 0: $$\mathbf{X'} = \mathbf{X} - \bar{x}$$

​

B. Standardization

Standardization puts all features on the same scale by dividing each zero-centered dimension by its standard deviation: $$\mathbf{X'} = \frac{\mathbf{X} - \bar{x}}{\sigma_{\mathbf{X}}}$$

​

C. Whitening

Whitening (or sphering) transforms data to have a covariance matrix equal to the identity matrix. Steps:

1. Zero-center the data
2. Decorrelate the data
3. Rescale the data

Decorrelation is achieved by projecting data onto the eigenvectors of the covariance matrix:

​

3. Image whitening

Zero Component Analysis (ZCA) whitening can be applied to preprocess image datasets: $$\mathbf{X}_{ZCA} = \mathbf{U} \cdot \text{diag}\left(\frac{1}{\sqrt{\text{diag}(\mathbf{S}) + \epsilon}}\right) \cdot \mathbf{U}^\text{T} \cdot \mathbf{X}$$ where $\mathbf{U}$ are the left singular vectors, $\mathbf{S}$ are the singular values, and $\epsilon$ is the whitening coefficient.

​

References

• Jarrett et al., 2009 - What is the best multi-stage architecture for object recognition?
• Krizhevsky, 2009 - Learning Multiple Layers of Features from Tiny Images
• LeCun et al., 2012 - Efficient BackProp
• Pal & Sudeep, 2016 - Preprocessing for image classification by CNNs
• Wan et al., 2013 - Regularization of Neural Networks using DropConnect

---