Skip to main content
In this chapter we examine training aspects of DNNs and investigate schemes that help avoid overfitting.

​
L2 Regularization

The most common form of regularization. It penalizes the squared magnitude of all parameters directly in the objective: λJpenalty=λ(∑lW(l)2)\lambda J_{\text{penalty}} = \lambda \left(\sum_l W_{(l)}^2 \right) where ll is the hidden layer index and WW is the weight tensor. L2 regularization heavily penalizes peaky weight vectors and prefers diffuse weight vectors. Due to multiplicative interactions between weights and inputs, this encourages the network to use all of its inputs a little rather than some of its inputs a lot.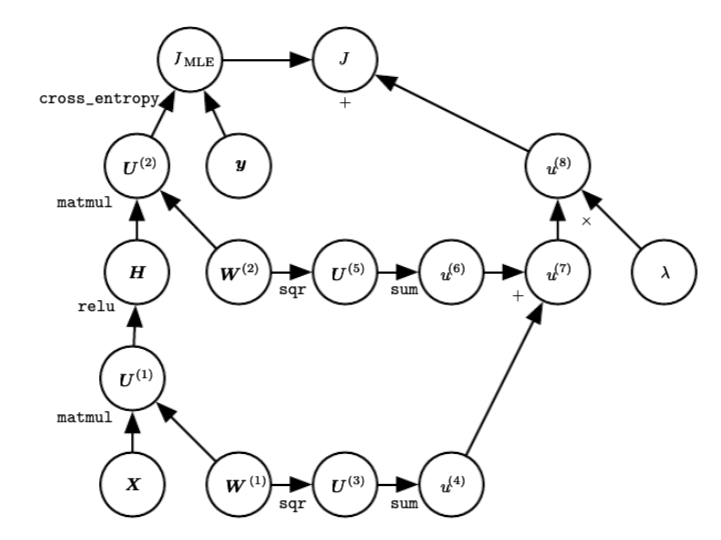
Regularized DNN computational graph

​
L1 Regularization

For each weight ww, add the term λ∣w∣\lambda \mid w \mid to the objective. L1 regularization leads weight vectors to become sparse during optimization (exactly zero). Neurons with L1 regularization use only a sparse subset of their most important inputs. Comparison:
  • L1: Sparse weights, feature selection
  • L2: Diffuse small weights, generally better performance
In practice, if you are not concerned with explicit feature selection, L2 regularization typically gives superior performance.

​
Dropout

An extremely effective regularization technique from Srivastava et al., 2014. During training, dropout keeps a neuron active with probability pp, or sets it to zero otherwise.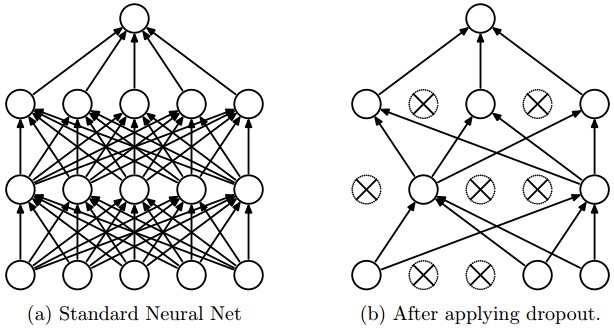
Dropout illustration

​
Standard Dropout

p = 0.5  # probability of keeping a unit active

def train_step(X):
    H1 = np.maximum(0, np.dot(W1, X) + b1)
    U1 = np.random.rand(*H1.shape) < p  # dropout mask
    H1 *= U1  # drop!
    # ... continue forward pass

def predict(X):
    H1 = np.maximum(0, np.dot(W1, X) + b1) * p  # scale activations
    # ... continue forward pass
At test time, we scale outputs by pp because neurons see all inputs. Expected output during training: px+(1−p)⋅0=pxpx + (1-p) \cdot 0 = px. Performs scaling at train time, leaving inference untouched: 
def train_step(X):
    H1 = np.maximum(0, np.dot(W1, X) + b1)
    U1 = (np.random.rand(*H1.shape) < p) / p  # scale during training
    H1 *= U1

def predict(X):
    H1 = np.maximum(0, np.dot(W1, X) + b1)  # no scaling needed
Inverted dropout is preferred because prediction code remains unchanged when tuning dropout placement or probability.

​
Early Stopping

Monitors validation loss during training and stops when validation error increases, retrieving the best model. This acts as an implicit L2 regularizer: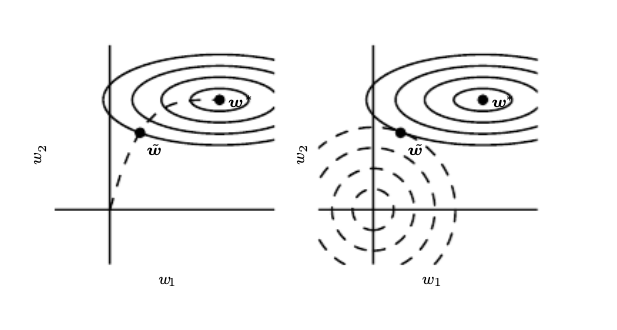
Early stopping vs L2

​
Practical Recommendations

  1. Use a single, global L2 regularization strength (cross-validated)
  2. Apply Dropout after all layers (default p=0.5p = 0.5, tune on validation)
  3. Combine with Batch Normalization (note: interesting interference between the two)
  4. Use Early Stopping with patience parameter

​
References

Edit this page on GitHub or file an issue.
Connect these docs to Claude, VSCode, and more via MCP for real-time answers.