Skip to main content

PCA Workshop

Comprehensive PCA tutorial covering dimensionality reduction, noise filtering, and eigenfaces

3D PCA Visualization

Interactive 3D visualizations with matplotlib and Plotly

​
Introduction

Consider an artificial data set constructed by taking one of the off-line digits, represented by a 64 x 64 pixel grey-level image, and embedding it in a larger image of size 100 x 100 by padding with pixels having the value zero (corresponding to white pixels) in which the location and orientation of the digit is varied at random, as illustrated in the figure below.
manifold-number-three
Each of the resulting images is represented by a point in the 100 x 100 = 10,000-dimensional data space. However, across a data set of such images, there are only three degrees of freedom of variability, corresponding to the vertical and horizontal translations and the rotations. The data points will therefore live on a subspace of the data space whose intrinsic dimensionality is three. For real digit image data, there will be a further degree of freedom arising from scaling. Moreover there will be multiple additional degrees of freedom associated with more complex deformations due to the variability in an individual’s writing as well as the differences in writing styles between individuals.

​
Geometric interpretation

Can we define PCA from a graphical point of view? This is shown in the next figure.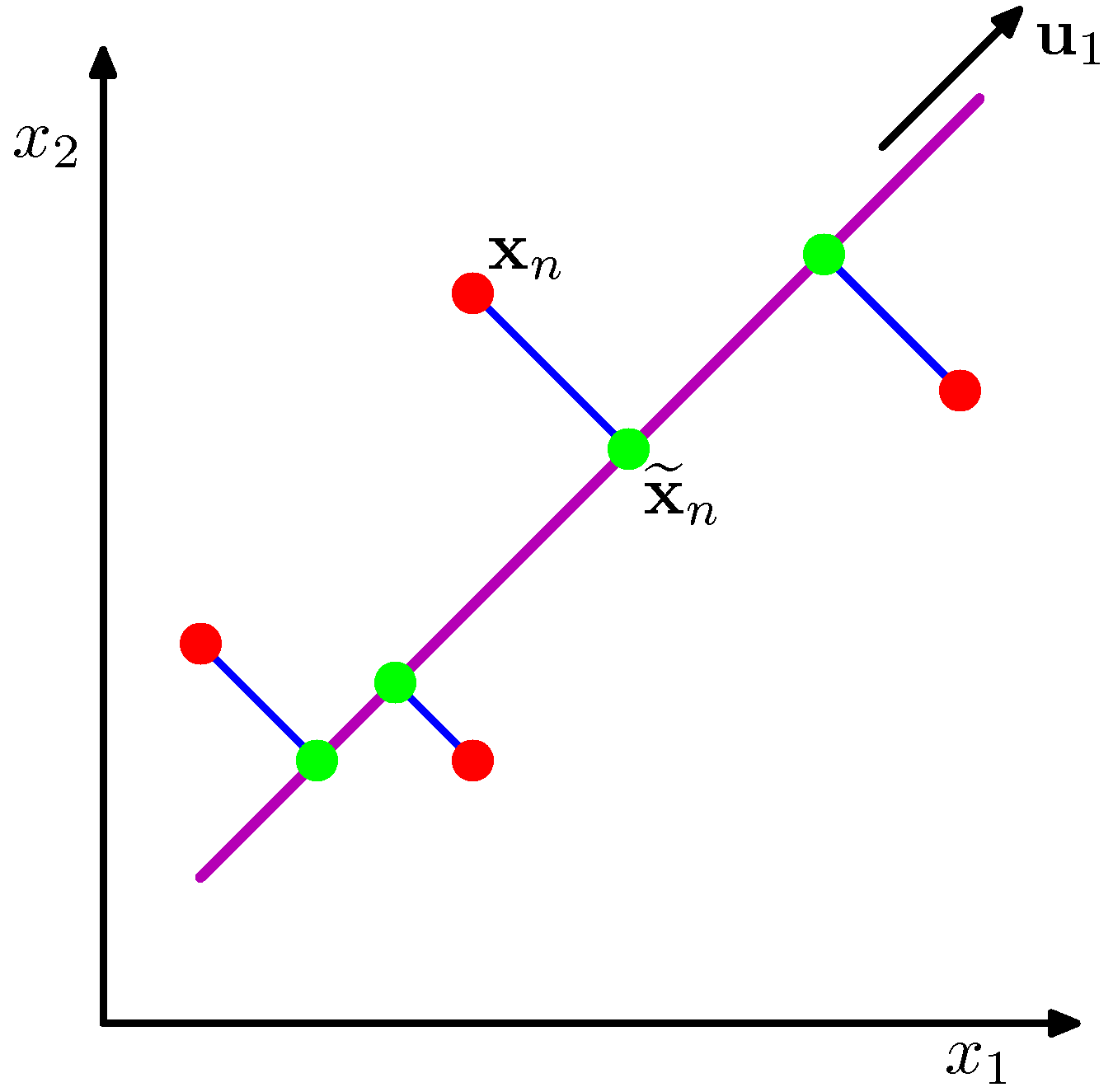
principal-subspace

​
Key concepts

PCA is fundamentally a dimensionality reduction algorithm, but it can also be useful as a tool for:
  • Visualization - Project high-dimensional data to 2D or 3D for plotting
  • Noise filtering - Reconstruct data using only the largest principal components
  • Feature extraction - Discover the most important directions of variance
  • Data compression - Represent data with fewer dimensions while preserving information

​
Applications covered in the notebooks

  1. Introducing PCA - Principal axes and explained variance
  2. PCA as dimensionality reduction - Projecting to lower dimensions
  3. PCA for visualization - Hand-written digits example
  4. Choosing the number of components - Explained variance ratio
  5. PCA as noise filtering - Denoising images
  6. Eigenfaces - Face recognition with PCA
Key references: (Bronstein et al., 2016; Chang et al., 2017; Zeng et al., 2016; Qi et al., 2016; Armeni et al., 2017)

​
References

  • Armeni, I., Sax, S., Zamir, A., Savarese, S. (2017). Joint 2D-3D-Semantic Data for Indoor Scene Understanding.
  • Bronstein, M., Bruna, J., LeCun, Y., Szlam, A., Vandergheynst, P. (2016). Geometric deep learning: going beyond Euclidean data.
  • Chang, A., Dai, A., Funkhouser, T., Halber, M., Nießner, M., et al. (2017). Matterport3D: Learning from RGB-D Data in Indoor Environments.
  • Qi, C., Su, H., Mo, K., Guibas, L. (2016). PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation.
  • Zeng, A., Song, S., Nießner, M., Fisher, M., Xiao, J., et al. (2016). 3DMatch: Learning Local Geometric Descriptors from RGB-D Reconstructions.
Edit this page on GitHub or file an issue.