Skip to main content
The discussion in the marginal distribution is equivalently applicable to the conditional distribution pmodel(y∣x,w)p_{model}(\mathbf y \mid \mathbf x, \mathbf w) which governs supervised learning, yy being the symbol of the label / target variable. Therefore all machine learning software frameworks offer excellent APIs on CE calculation. L(w)=−Ex,y∼p^datalog⁡pmodel(y∣x;w)L(\mathbf w) = - \mathbb{E}_{\mathbf x, \mathbf y \sim \hat p_{data}} \log p_{model}(\mathbf y \mid \mathbf x; \mathbf w) The attractiveness of the ML solution is that the CE (also known as log-loss) is general and we don’t need to re-design it when we change the model.

​
Visualizing the regression function - the conditional mean

It is now instructive to go over an example to understand that even the plain-old mean squared error (MSE), the objective that is common in the regression setting, falls under the same umbrella - it’s the cross entropy between p^data\hat p_{data} and a Gaussian model. Please follow the discussion associated with Section 5.5.1 of Ian Goodfellow’s Deep Learning book or section 20.2.4 of Russell & Norvig’s book and consider the following figure for assistance to visualize the relationship of 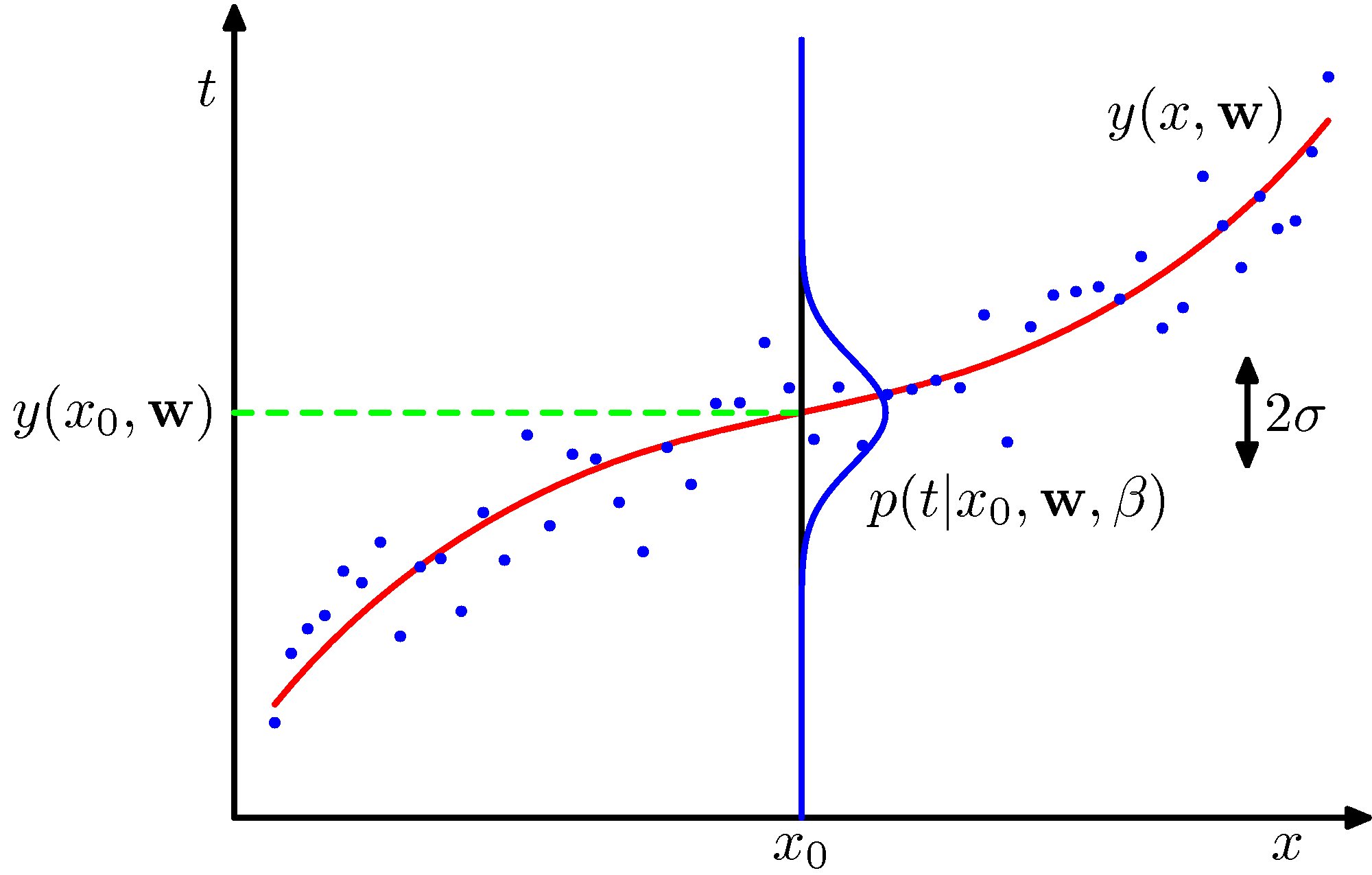pdatap_{data} and pmodelp_{model}.
Conditional Model Gaussian

​
Key Insight: MSE as Cross-Entropy

When we assume the model distribution is Gaussian: pmodel(y∣x;w)=N(y∣f(x;w),σ2)p_{model}(\mathbf y \mid \mathbf x; \mathbf w) = \mathcal{N}(\mathbf y \mid f(\mathbf x; \mathbf w), \sigma^2) The negative log-likelihood becomes: −log⁡pmodel(y∣x;w)=12σ2(y−f(x;w))2+const-\log p_{model}(\mathbf y \mid \mathbf x; \mathbf w) = \frac{1}{2\sigma^2}(\mathbf y - f(\mathbf x; \mathbf w))^2 + \text{const} This is proportional to the mean squared error (MSE). Therefore, minimizing MSE is equivalent to maximum likelihood estimation under a Gaussian noise assumption. Key references: (Frazier, 2018; Bengio et al., 2015; Blei et al., 2016; Martin-Maroto & Polavieja, 2018; Beygelzimer et al., 2015)

​
References

  • Bengio, E., Bacon, P., Pineau, J., Precup, D. (2015). Conditional Computation in Neural Networks for faster models.
  • Beygelzimer, A., Hazan, E., Kale, S., Luo, H. (2015). Online Gradient Boosting.
  • Blei, D., Kucukelbir, A., McAuliffe, J. (2016). Variational Inference: A Review for Statisticians.
  • Frazier, P. (2018). A Tutorial on Bayesian Optimization.
  • Martin-Maroto, F., Polavieja, G. (2018). Algebraic Machine Learning.
Edit this page on GitHub or file an issue.