Skip to main content
This example demonstrates stochastic gradient descent (SGD) for polynomial regression on a synthetic sinusoidal dataset. We explore regularization and hyperparameter tuning using Optuna.

​
Dataset Generation

We create a toy dataset by sampling from a sinusoidal function with added Gaussian noise: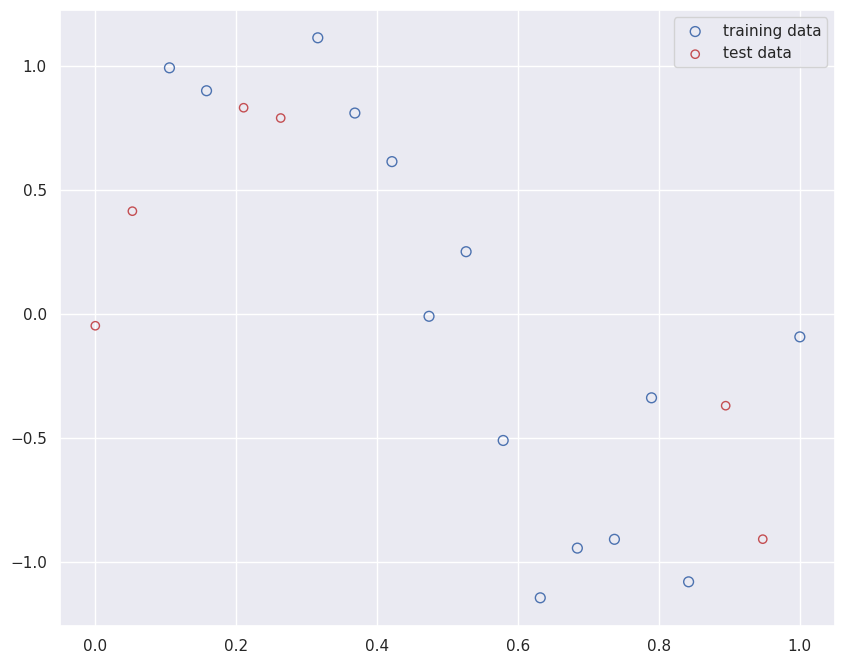 
import numpy as np
from sklearn.model_selection import train_test_split

def create_toy_data(func, sample_size, std, domain=[0, 1]):
    rng = np.random.default_rng()
    x = np.linspace(domain[0], domain[1], sample_size)
    np.random.shuffle(x)
    y = func(x) + rng.normal(scale=std, size=x.shape)
    return x, y

def sinusoidal(x):
    return np.sin(2 * np.pi * x)

m = 20
x, y = create_toy_data(sinusoidal, m, 0.25)

# Reshape and split
x = x.reshape(-1, 1)
x_train, x_test, y_train, y_test = train_test_split(
    x, y, test_size=0.3, random_state=42
)
Training and Test Data

​
Polynomial Feature Transformation

We use polynomial features to enable fitting complex curves with linear regression: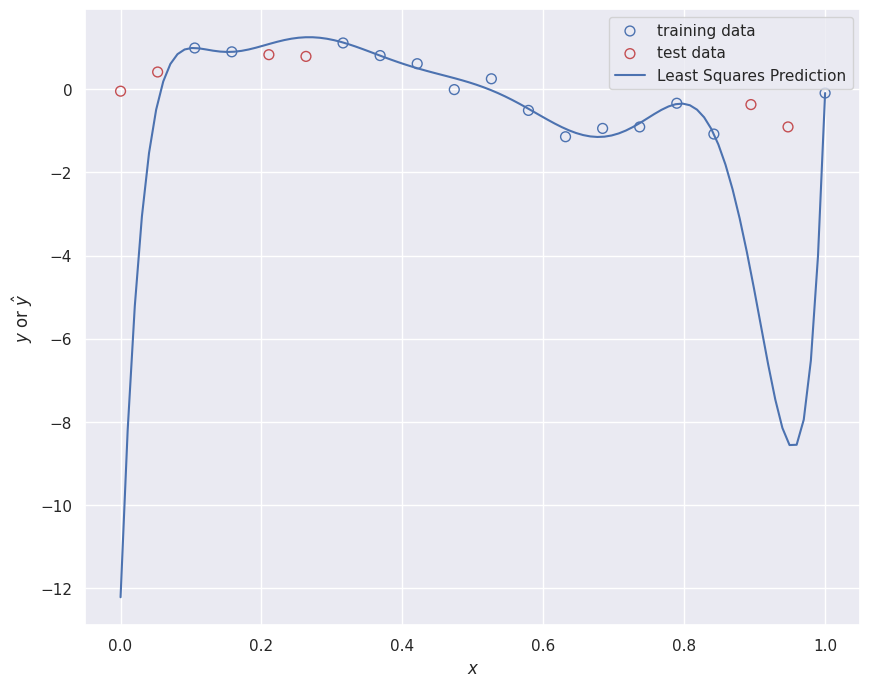 
from prml.preprocess import PolynomialFeature

M = 9  # Polynomial degree
feature = PolynomialFeature(M)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
Least Squares Polynomial Fit

​
SGD Implementation with Regularization

The SGD loop implements mini-batch gradient descent with L2 regularization: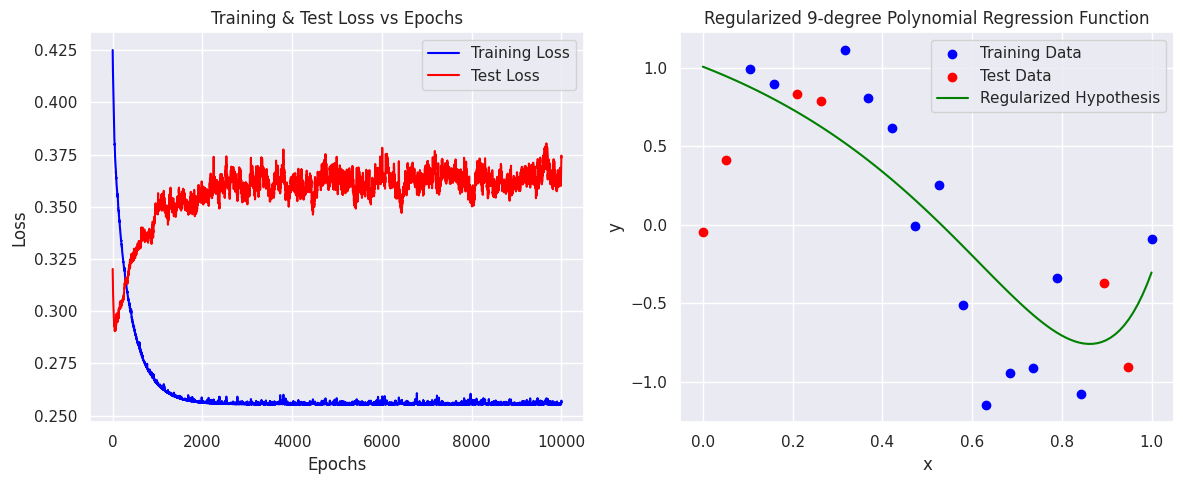 
def sgd_loop(X_train, y_train, X_test, y_test, w,
             learning_rate, epochs, lambda_reg, n_samples, batch_size=1):
    losses = []
    test_losses = []

    for epoch in range(epochs):
        for i in range(0, n_samples, batch_size):
            # Select mini-batch
            batch_indices = np.random.choice(n_samples, batch_size, replace=False)
            xi = X_train[batch_indices]
            yi = y_train[batch_indices]

            # Prediction and error
            y_pred = np.dot(xi, w)
            error = y_pred - yi

            # Gradient with L2 regularization
            dw = (2 / batch_size) * (xi.T @ error).flatten() + 2 * lambda_reg * w

            # Update weights
            w -= learning_rate * dw

        # Compute losses
        y_hat_train = X_train @ w
        loss = np.mean((y_hat_train - y_train) ** 2) + lambda_reg * np.sum(w**2)
        losses.append(loss)

        y_hat_test = X_test @ w
        test_loss = np.mean((y_hat_test - y_test) ** 2) + lambda_reg * np.sum(w**2)
        test_losses.append(test_loss)

    return min(test_losses)
SGD Training Results

​
Hyperparameter Tuning with Optuna

We use Optuna to find the optimal regularization parameter 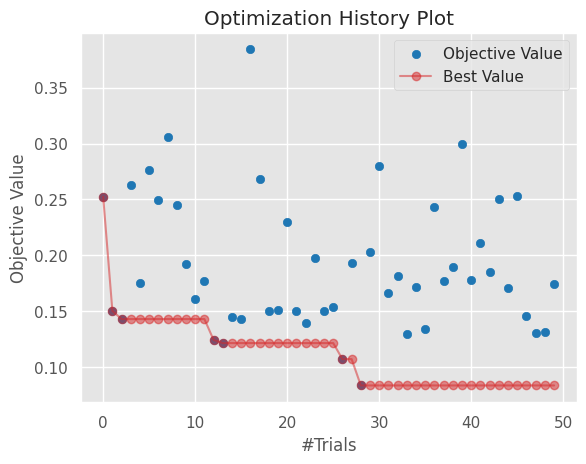λ\lambda: 
import optuna

def objective(trial):
    # Sample lambda from log-uniform distribution
    lambda_reg = trial.suggest_loguniform("lambda_reg", 1e-4, 1.0)

    # Initialize weights
    w = np.random.randn(10)
    batch_size = len(y_train)

    # Run SGD and return test loss
    min_test_loss = sgd_loop(
        X_train=X_train, y_train=y_train,
        X_test=X_test, y_test=y_test,
        w=w, learning_rate=0.01, epochs=10000,
        lambda_reg=lambda_reg, n_samples=len(y_train),
        batch_size=batch_size,
    )
    return min_test_loss

# Run optimization
study = optuna.create_study(direction="minimize")
study.optimize(objective, n_trials=50)

print(f"Best lambda_reg: {study.best_params['lambda_reg']}")
print(f"Best test loss: {study.best_value}")
Optuna Optimization History

​
Key Takeaways

  1. Regularization prevents overfitting: High-degree polynomials (M=9) can memorize training data. L2 regularization constrains the weights to improve generalization.
  2. Learning rate matters: Too high causes divergence, too low causes slow convergence. A value of 0.01 works well for this problem.
  3. Batch size trade-offs: Larger batches give more stable gradients but slower updates per epoch. Full-batch gradient descent (batch_size = n_samples) is used for hyperparameter search stability.
  4. Automated tuning: Optuna efficiently searches the hyperparameter space using Bayesian optimization, finding good regularization values without manual grid search.
Key references: (Keskar et al., 2016; Keskar et al., 2016; Martin-Maroto & Polavieja, 2018; Bottou et al., 2016; Andrychowicz et al., 2016)

​
References

  • Andrychowicz, M., Denil, M., Gomez, S., Hoffman, M., Pfau, D., et al. (2016). Learning to learn by gradient descent by gradient descent.
  • Bottou, L., Curtis, F., Nocedal, J. (2016). Optimization Methods for Large-Scale Machine Learning.
  • Keskar, N., Mudigere, D., Nocedal, J., Smelyanskiy, M., Tang, P. (2016). On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima.
  • Keskar, N., Mudigere, D., Nocedal, J., Smelyanskiy, M., Tang, P. (2016). On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima.
  • Martin-Maroto, F., Polavieja, G. (2018). Algebraic Machine Learning.
Edit this page on GitHub or file an issue.