Skip to main content
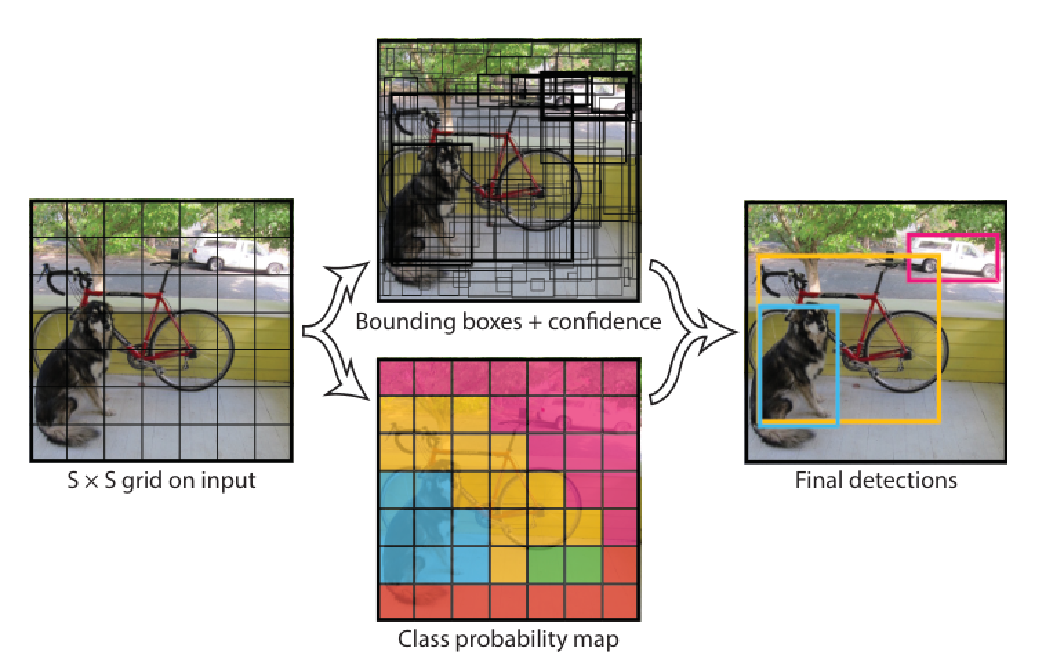
Visual explanation of YOLOv1 operation As shown in (see figure above), YOLOv1 partitions the input image into an S×SS\times S grid. If the center of an object falls in cell ii, that cell is responsible for predicting it. Each grid cell outputs BB bounding-box hypotheses and one set of class probabilities over CC classes, yielding an S×S×(B⋅5+C)S\times S\times (B\cdot 5 + C) tensor. For VOC, S=7S=7, B=2B=2, C=20⇒7×7×30C=20 \Rightarrow 7\times7\times 30. Each bounding box prediction carries five numbers (x,y,w,h,confidence),(x, y, w, h, \text{confidence}), where (x,y)(x,y) are the box-center offsets relative to the owning cell, and (w,h)(w,h) are normalized by image width/height. The confidence is intended to equal the IoU between the predicted box and the closest ground-truth box (and be 00 when no object is present).

​
Class-specific confidence at test time

At inference we combine per-cell conditional class probabilities with the per-box confidence to score each box for each class: Pr⁡(Classi∣Object)⋅Pr⁡(Object)⋅IoUpredtruth  =  Pr⁡(Classi)⋅IoUpredtruth.(1)\Pr(\text{Class}_i \mid \text{Object}) \cdot \Pr(\text{Object})\cdot \text{IoU}_{\text{pred}}^{\text{truth}} \;=\; \Pr(\text{Class}_i)\cdot \text{IoU}_{\text{pred}}^{\text{truth}}. \tag{1} This produces class-specific confidence scores used before NMS.

​
Network architecture and activations

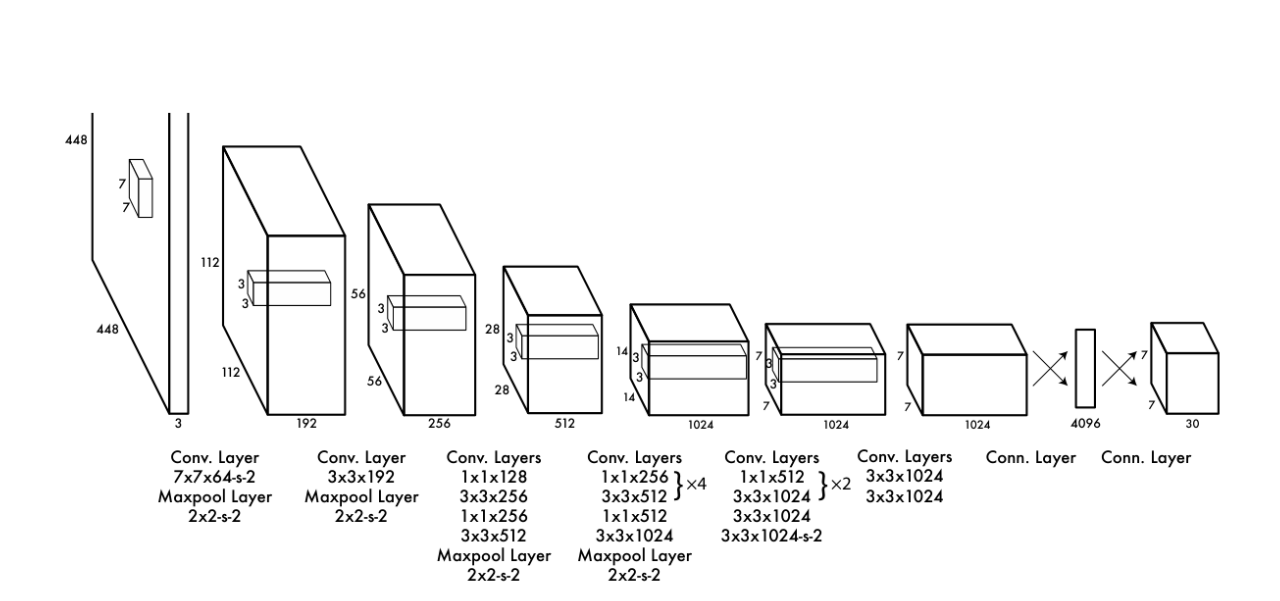
YOLOv1 Architecture As shown in (see figure above), the detector is a single CNN: 24 conv layers + 2 fully-connected layers; early layers extract features, FC layers map to the S×S×(B⋅5+C)S\times S\times (B\cdot5+C) output. A fast variant reduces conv depth. Final layer uses a linear activation; all others use leaky ReLU ϕ(x)={x,x>0,0.1x,otherwise.(2)\phi(x)= \begin{cases} x, & x>0,\\ 0.1x, & \text{otherwise.} \end{cases} \tag{2} Coordinates are normalized as described above.

​
Training targets and responsibility

Because each cell predicts BB boxes, YOLO assigns “responsibility” to exactly one of the BB predictors for a given object: the predictor whose current box has the highest IoU with that object’s ground-truth. This specialization improves recall. Consequence for targets:
  • Only the responsible predictor for a cell/object receives coordinate and objectness regression targets for that object.
  • The other predictor(s) in that cell are trained toward “no object” for confidence, reducing spurious positives.
That assignment happen per-iteration using the model’s current boxes.

​
The multi-part loss

YOLOv1 optimizes a sum-squared error over location, size, objectness (confidence), and classification, with two balancing coefficients λcoord\lambda_{\text{coord}} and λnoobj\lambda_{\text{noobj}}. To de-emphasize scale sensitivity, the loss regresses w,h\sqrt{w},\sqrt{h} instead of w,hw,h. L=  λcoord∑i=1S2∑j=1B1ijobj[(xi−x^i)2+(yi−y^i)2]+λcoord∑i=1S2∑j=1B1ijobj[(wi−w^i)2+(hi−h^i)2]+∑i=1S2∑j=1B1ijobj(Ci−C^i)2+λnoobj∑i=1S2∑j=1B1ijnoobj(Ci−C^i)2+∑i=1S21iobj∑c∈C(pi(c)−p^i(c))2.\begin{aligned} \mathcal{L} = \;& \lambda_{\text{coord}} \sum_{i=1}^{S^2} \sum_{j=1}^{B} \mathbf{1}^{\text{obj}}_{ij} \Big[(x_i-\hat{x}_i)^2 + (y_i-\hat{y}_i)^2\Big] \\ &+ \lambda_{\text{coord}} \sum_{i=1}^{S^2} \sum_{j=1}^{B} \mathbf{1}^{\text{obj}}_{ij} \Big[\big(\sqrt{w_i}-\sqrt{\hat{w}_i}\big)^2 + \big(\sqrt{h_i}-\sqrt{\hat{h}_i}\big)^2\Big] \\ &+ \sum_{i=1}^{S^2}\sum_{j=1}^{B} \mathbf{1}^{\text{obj}}_{ij}\big(C_i-\hat{C}_i\big)^2 + \lambda_{\text{noobj}} \sum_{i=1}^{S^2}\sum_{j=1}^{B} \mathbf{1}^{\text{noobj}}_{ij}\big(C_i-\hat{C}_i\big)^2 \\ &+ \sum_{i=1}^{S^2}\mathbf{1}^{\text{obj}}_{i} \sum_{c\in\mathcal{C}}\big(p_i(c)-\hat{p}_i(c)\big)^2. \end{aligned} Here 1ijobj=1\mathbf{1}^{\text{obj}}_{ij}=1 iff predictor jj in cell ii is responsible for some object; 1ijnoobj=1\mathbf{1}^{\text{noobj}}_{ij}=1 for “no object” cases; λcoord=5\lambda_{\text{coord}}=5 and λnoobj=0.5\lambda_{\text{noobj}}=0.5. Classification loss is applied only when a cell contains an object.

​
Optimization details

Typical training recipe (VOC): ~135 epochs, batch size 64, momentum 0.9, weight decay 5 ⁣× ⁣10−45\!\times\!10^{-4}. LR warmup from 10−310^{-3} to 10−210^{-2}, then 10−210^{-2} for 75 epochs, 10−310^{-3} for 30, 10−410^{-4} for 30. Regularization via dropout (rate 0.5 after first FC) and data augmentation (random scale/translation up to 20%, exposure/saturation jitters in HSV up to 1.5×).

​
End-to-end inference

  1. Preprocess: resize the image (e.g., to 448×448448\times 448) and forward once through the CNN.
  2. Decode raw outputs:
    • For each cell ii and predictor jj: convert normalized (x,y,w,h)(x,y,w,h) to image coordinates; take the predicted confidence CijC_{ij}.
    • Combine with class probabilities pi(c)p_i(c) using Eq. (1) to get class-specific scores sijc=pi(c)⋅Cijs_{ijc} = p_i(c)\cdot C_{ij}.
  3. Filter and suppress:
    • Discard low-score boxes.
    • Perform non-max suppression per class. While not as critical as in proposal-based pipelines, NMS adds ~2–3 mAP points by removing duplicates from neighboring cells.

​
Strengths and limitations

  • One-shot, global reasoning; extremely fast.
  • Different error profile vs. R-CNN family (fewer background false positives, more localization errors).
  • Limitations: fixed grid capacity (crowded small objects), coarse features due to downsampling, and sensitivity to small-box localization.
  • Grid cell owns an object if the object’s center falls inside.
  • Exactly one predictor per owned object learns its geometry (IoU-based responsibility).
  • Confidence == objectness ×\times IoU; class probs are cell-level. Eq. (1) fuses them into a per-class score.
  • Loss trades off localization, objectness, and classification with λcoord,λnoobj\lambda_{\text{coord}},\lambda_{\text{noobj}}; sizes use square-root to temper scale effects. Eq. (3).

​
PyTorch notebooks

The following notebooks progressively build a complete YOLOv11 anchor-free detector from scratch in PyTorch.

Data Pipeline

COCO data loading, letterbox resizing, mosaic augmentation, and multi-scale target encoding for anchor-free detection.

Backbone

Conv-BN-SiLU blocks, Bottleneck, C3k2 (CSP), SPPF, and the full backbone producing P3/P4/P5 features.

Neck and Head

FPN top-down and PAN bottom-up feature aggregation, C2PSA attention, decoupled anchor-free head with DFL.

Loss and Training

IoU variants (GIoU/DIoU/CIoU), Task-Aligned Learning, BCE + CIoU + DFL composite loss, training loop.

Inference and Evaluation

Prediction decoding, NMS from scratch, COCO mAP evaluation, Grad-CAM visualization.
Key references: (Redmon et al., 2015; Redmon & Farhadi, 2016; Liu et al., 2015; Canziani et al., 2016; Godard et al., 2016)

​
References

  • Canziani, A., Paszke, A., Culurciello, E. (2016). An Analysis of Deep Neural Network Models for Practical Applications.
  • Godard, C., Aodha, O., Brostow, G. (2016). Unsupervised Monocular Depth Estimation with Left-Right Consistency.
  • Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S., et al. (2015). SSD: Single Shot MultiBox Detector.
  • Redmon, J., Divvala, S., Girshick, R., Farhadi, A. (2015). You only look once: Unified, real-time object detection.
  • Redmon, J., Farhadi, A. (2016). YOLO9000: Better, Faster, Stronger.
Edit this page on GitHub or file an issue.